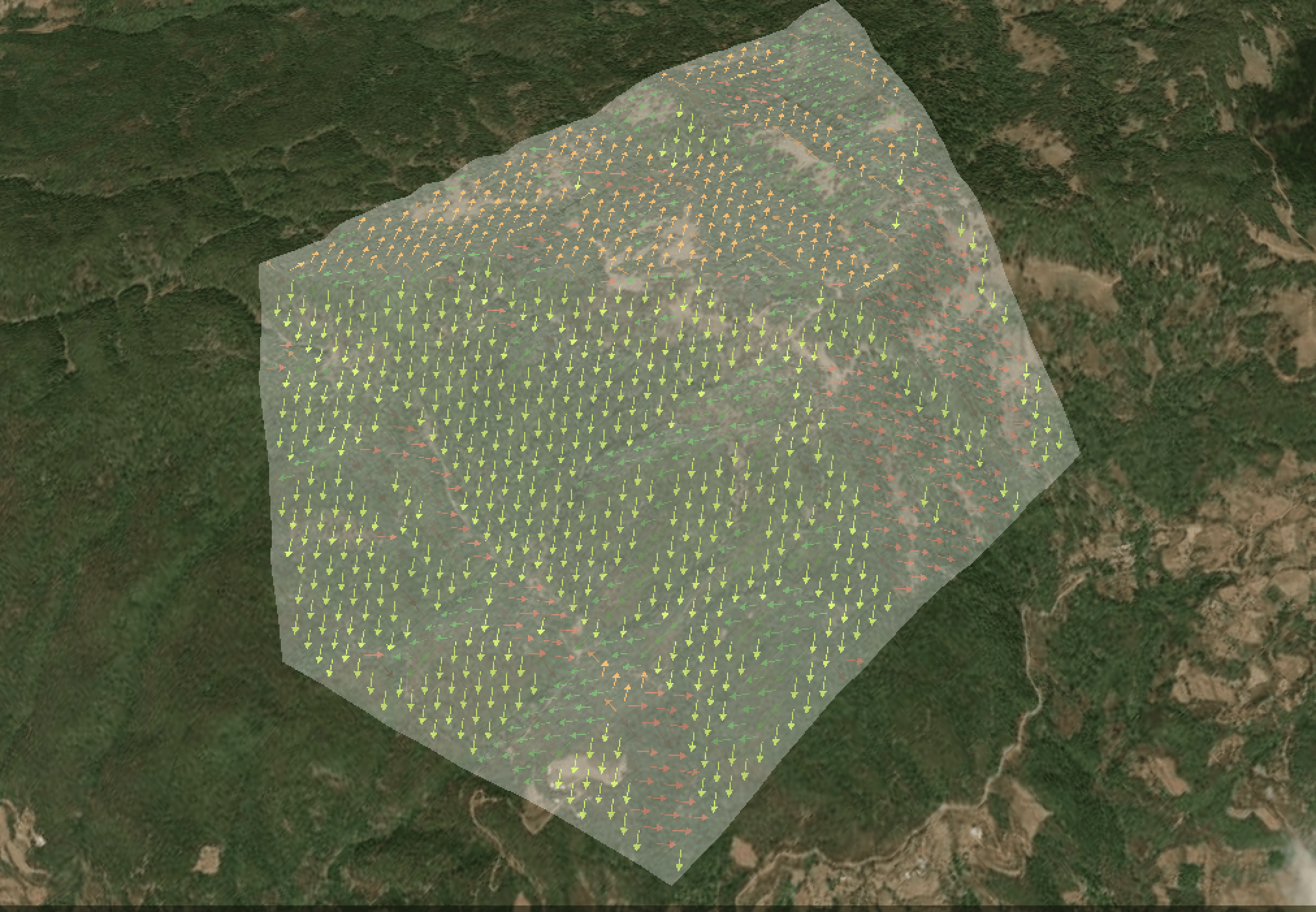
准备数据

制作网格

要计算坡向，首先先获取感兴趣区域的DEM数据，但是在Cesium里不能直接获取，需要借助地形，绘制一个用于模拟栅格数据的网格，然后获取网格内各个点的三维坐标。

这个步骤可以借助一个开源库来实现——turf，首先获取感兴趣区域的多边形的坐标，然后计算多边形的最小包围矩形框，然后根据区域大小，设置合适的网格变长，示例代码如下。

# 获取包围矩形
const analyseArea = [[[100, 32], [110, 33], [103, 35], [103, 32]] // 分析区域多边形示例坐标，非图片展示位置
let AOI = turf.polygon(analyseArea); // 创建多边形
let box = turf.bbox(AOI); // 计算矩形

// 创建网格
let grid = turf.squareGrid(box, 50, { units: 'meters' });
// 因为包围矩形内部分网格并不在分析区内，所以过滤掉
  const filteredGrid = turf.featureCollection(
    grid.features.filter(feature => {
      return turf.booleanWithin(feature, AOI);
    })
  );

   // 将网格以实体形式添加到cesium里查看
  filteredGrid.features.forEach(feat => {
    const coord = feat.geometry.coordinates[0];
    const centroid = turf.centroid(feat).geometry.coordinates;
    let featCarte = [];
    for (let i = 0; i < coord.length - 1; i++) {
      featCarte.push(Cesium.Cartesian3.fromDegrees(coord[i][0], coord[i][1]));
    }
    window.viewer.entities.add({
      polyline: {
        positions: featCarte,
        material: Cesium.Color.RED,
        clampToGround: true,
      },
    });
   });

网格效果

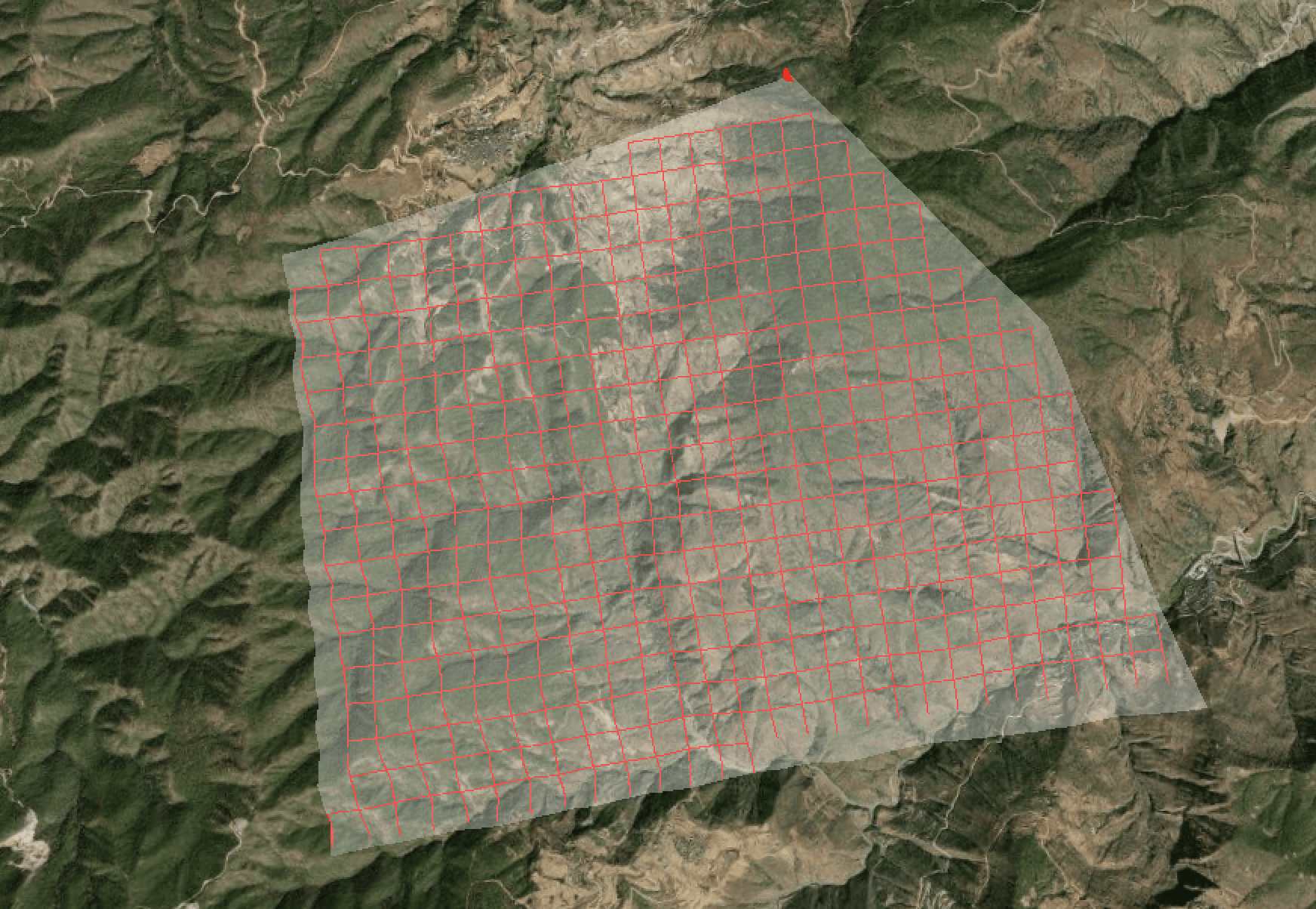
获取网地形高程

计算网格的四个中点后，加上四个顶点及中心点，全部转为笛卡尔三维坐标，接着使用Cesium的API获取这9个点点地形高度。

// ...省略坐标转换
let positions = [[这里共有9个地理坐标点，按顺序前四个为顶点，接着四个边中点，最后中心点],...]// 所有单元格坐标转换后的数组，二维数组

 // 构造promise集合
let promiseAll = positions.map(cell => {
  let cartos = cell.map(item => Cesium.Cartographic.fromCartesian(item));
  return Cesium.sampleTerrainMostDetailed(window.viewer.terrainProvider, cartos);
});

可视化

在这一步获取到高程之后，计算单元格边点与中心点点高差后并计算角度，之后将结果添加到cesium中，通过设置贴图的方式展示坡向分布。

// 统一处理所有promise
Promise.allSettled(promiseAll)
.then(res => {
  res.forEach(item => {
    const { status, value } = item;
    if (status === 'fulfilled') {
      // 最后一个为中心点，求倒数第二点到第一个点直接最高的点
      let highest = value[0];
      const centroid = value[value.length - 1];
      let start, end;
      for (let i = 1; i < value.length - 1; i++) {
        if (value[i].height > highest.height) {
          highest = value[i];
        }
      }
      // 高程最大的点作为起点
      if (centroid.height > highest.height) {
        start = centroid;
        end = highest;
      } else {
        start = highest;
        end = centroid;
      }
      const angle = calculateAzimuth(start, end).toFixed(0);
      // 构造矩形实体
      window.viewer.entities.add(
        new Cesium.Entity({
          rectangle: {
            coordinates: Cesium.Rectangle.fromCartographicArray(value.slice(0, 4)),
            material: new Cesium.ImageMaterialProperty({
              image: './static/arrow.png',
              transparent: true,
            }),
            rotation: Cesium.Math.toRadians(angle), // 设置旋转角度
            stRotation: Cesium.Math.toRadians(angle), // 纹理坐标旋转
          },
        })
      );
    }
  });
})

// 计算两个坐标点构成的线段的方位角
function calculateAzimuth(point1, point2) {
  const lon1 = point1.longitude;
  const lat1 = point1.latitude;
  const lon2 = point2.longitude;
  const lat2 = point2.latitude;
  const dLon = lon2 - lon1;
  const x = Math.sin(dLon) * Math.cos(lat2);
  const y = Math.cos(lat1) * Math.sin(lat2) - Math.sin(lat1) * Math.cos(lat2) * Math.cos(dLon);
  let azimuth = Math.atan2(x, y);
  azimuth = Cesium.Math.toDegrees(azimuth);
  if (azimuth < 0) {
    azimuth += 360;
  }
  return azimuth;
}

代码注意的点

添加实体的时候，为了设置贴图的旋转角度，必须指定几何类型为矩形

贴图图片材质

最终的效果

可以给材质设置随机颜色

rectangle: {
  coordinates: Cesium.Rectangle.fromCartographicArray(value.slice(0, 4)),
  material: new Cesium.ImageMaterialProperty({
    image: './static/arrow.png',
    color: Cesium.Color.fromRandom({ alpha: 0.8 });
    transparent: true,
  }),
  rotation: Cesium.Math.toRadians(angle), // 设置旋转角度
  stRotation: Cesium.Math.toRadians(angle), // 纹理坐标旋转
},

简要总结

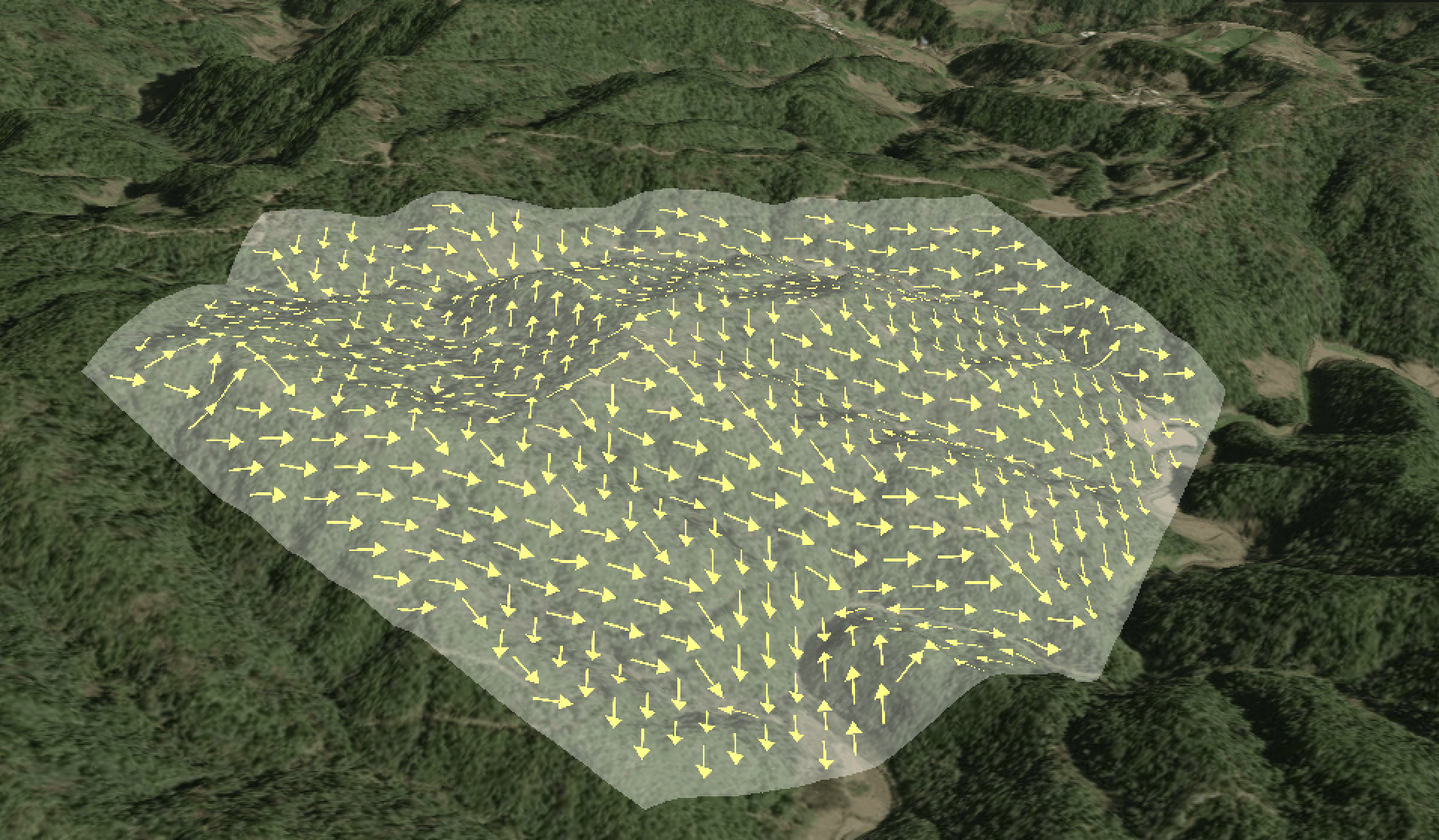
基本反映了坡向的分布，但是，

这个方案在获取地形的时候，非常耗时好内存，特别是在分析大范围区域时，网格的数量特别巨大。
坡向准确性低，因为我只计算了周围的八个主要方向的点。

单元格计算坡向目前使用图形1的结构，图形2效果可能会好一点

目录

准备数据

制作网格

获取网地形高程

可视化

简要总结